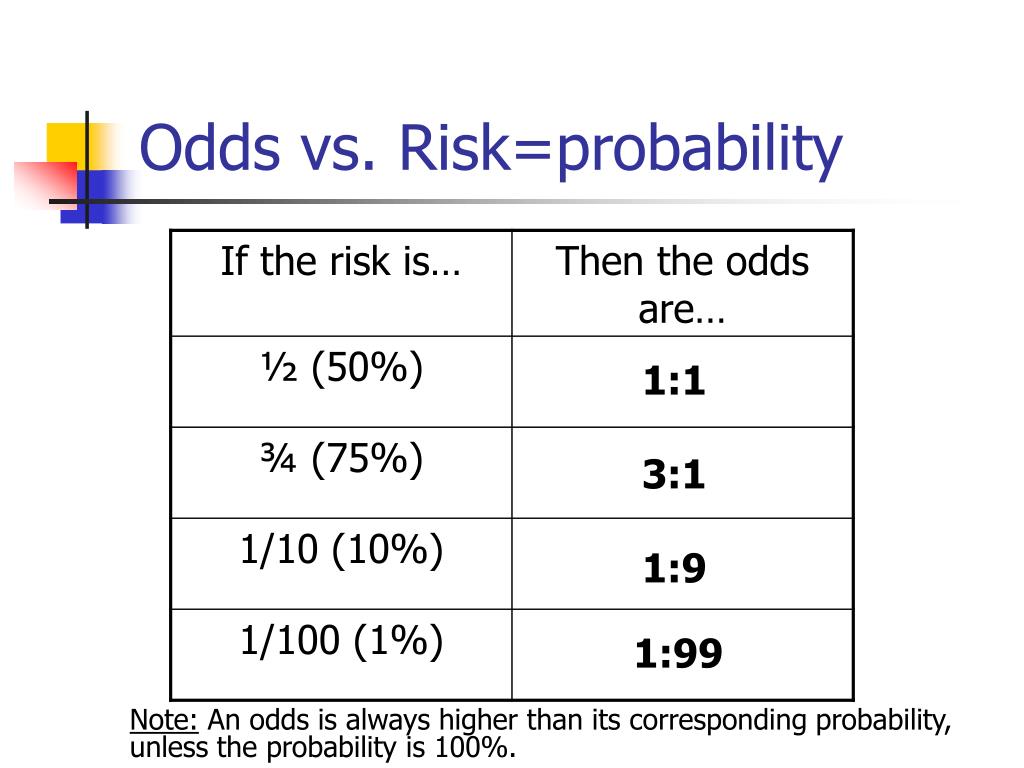
Odds is a see also of probability As nouns the difference between odds and probability is that odds is the ratio of the probabilities of an event happening to that of it not happening while probability is the state of being probable; Odds vs Probability Probability is a mathematical assumption of chance that can be calculated using an equation The equation measures the chances for an event to occur against the total number of chances that occurrence may produceHome > Online Casinos > Casino Articles > House Odds vs True Odds House Odds vs True Odds I've written about house odds vs true odds before, but not in so many words You can read about the basics of probability on this site, and you can read about the house edgeBut another way of looking at these concepts is by examining the difference between payoff odds and true odds

Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science
Odds and probability
Odds and probability- The probability of drawing a red card from a standard deck of cards is 26/52 (50 percent) The probability of drawing a club from that deck is 13/52 (25 percent) And so on The odds for an event is the ratio of the number of ways the event can occur to the number of ways it Odds and Probability In mathematical concepts, we use odds and probability calculations in many ways like while solving the Playing Cards Probability and calculating the problems like the trains may be late, it may take an hour, to reach home and so forth Here we will be discussing Odds & Probability Topic The definitions for both are given in this article



Chapter 4 Introduction To Probability Statistics At Eastside Prep
Odds vs Probability A good way to understand the difference between odds and probability is to imagine rolling a die and hoping to land on a two The odds of rolling the two are 1 to 5 One representing the chance of landing on the two, and five representing the alternative possibilities of landing on one of the other sides The probability Say for example the odds are represented as 25, this would imply that for every 1 you wager, you will gain a profit of 15 if the outcome was in your favor Here, to convert odds ratio to probability in sports handicapping, we would have the following equation (1 / the decimal odds) * 100 or (1 / 25) * 100 The odds of an event of interest occurring is defined by odds = p/(1p) where p is the probability of the event occurring So if p=01, the odds are equal to 01/09=0111 (recurring) So here the probability (01) and the odds (0111) are quite similar Indeed whenever p is small, the probability and odds will be similar
The odds in favor of an event is the ratio of the number of ways the outcome can occur to the number of ways the outcome cannot occur # of ways the event CAN occur # of ways the event CANNOT occur This is actually a lot easier than probability So, let's take a look at an exampleIn this matchup, there is a big difference between the two odds, indicating a much higher probability of Duke winning the game and advancing to the next round of the NCAA TournamentA probability is always expressed as a number between 0 and 1 Odds on the other hand are expressed as the likelihood of an event occurring divided by the likelihood of it not occurring Probabilities of 0 are the same as odds of 0 If the probability is between 0 and 05, the odds
Calculating Probability Given Odds To calculate Intuitively, it's difficult to estimate the most likely success, but with our dice probability calculator, it takes only a blink of an eye to evaluate all the probabilities The resulting values are P₁ = for 10 sided dice P₂ = Probability compares the number of successes to the total number of attempts made The odds in favor of an event compares the number of successes to the number of failures In what follows, we will see what this means in greater detail First, we consider a little notation




Probability Odds Odds Ratio Youtube




Relation Between Probability And Odds At Different Values Of Probability Download Scientific Diagram
Playing 2 vs 1 dice I get around a % win rate Now to my problem, if I want to calculate the amount needed to always win as the house, the odds of losing (for the player) needs to be higher than the potentialwinningriskamount Probability has a limited range from zero to one Odds has an infinite range The probability of something happening is always less than the odds of it happening (assuming the probability is nonzero) The smaller the probability, the more similar probability and odds The higher the number, the greater the probability of the outcome Using an example of decimal odds, a candidate has 2 odds to win the next election If so, the implied probability is 4545%




Odds Introduction Arbital




Probability And Odds Quiz Topics Spin A Spinner Probability Draw From A Bag Of Balls Odds Counting Prin Third Grade Math Worksheets Math Probability
The differences between odds and probability are discussed in the points given below The term 'odds' is used to describe that if there are any chances of the occurrence of an event or not As against, While odds are expressed in the ratio, the probability is either written in percentage form orOut of 5 times, 1 time will be the event and 4 times will be the nonevent, odds = 025 Odds = 1/5 / 4/5 = 1/4 = 025; Odds can be expressed as a ratio of the probability an event will happen divided by the probability an event won't happen Odds in favor of A = A / (1 A), usually simplified to lowest terms, For instance, if the probability of an event occurring is 075, then the odds for it happening are 075/025 = 3/1 = 3 to 1 for, while the probability that it doesn't occur is 1 to 3 against




Binary Logistic Regression With Odds Ratios Calculated For The Download Table




Statistics 12 Probability Vs Odds Stats Seandolinar Com
Of probability, chances and odds are not the same For instance, the odds in favor of A are P(A) / P(Ac) = (3/4)/(1/4) = 3/1 It is said that the odds in favor of A are 31 or that A is an event twice as likely as "not A" Therefore, the odds of A occurring are expressed in the scale of the probability of "A not occurring"Calculating the odds without the number of subjects by the ratio of the number of events (1) by the number of nonevents (4) odds = 1/4 = 025;Many people wrongfully assume odds and probabilities are the same thingThey're definitely not, as there's a significant difference between saying there are
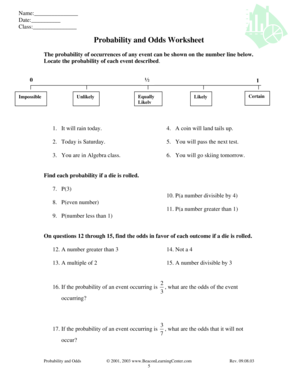



Probability And Odds Worksheet Fill Online Printable Fillable Blank Pdffiller



Odds Ratio For A Simple Distribution Jmp User Community
Converting Odds to Probability Simply add the 2 components of the odds together to make a new denominator, and use the old numerator eg If the odds are 35, or 3 to 5, the probability is 3 ÷ (35) = 3/8 = 375% Converting Probability to Odds Take the probability, and divide it by its compliment = (1itself) egProbability theory is an interesting area of statistics concerned with the odds or chances of an event happening in a trial, eg getting a six when a dice is thrown or drawing an ace of hearts from a pack of cards To work out odds, we also need to have anHow to find probability and odds and the difference between the two We also discuss experimental probablility, theoretical probability, odds in favor, and




Statquest Odds And Log Odds Clearly Explained Youtube



Chapter 4 Introduction To Probability Statistics At Eastside Prep
In statistics, the odds for or odds of some event reflect the likelihood that the event will take place, while odds against reflect the likelihood that it will not In gambling, the odds are the ratio of payoff to stake, and do not necessarily reflect exactly the probabilitiesOdds, are given as (chances for success) (chances against success) or vice versa If odds are stated as an A to B chance of winning then the probability of winning is given as P W = A / (A B) while the probability of losing is given as P L = B / (A B) For example, you win a game if you pull an ace out of a full deck of 52 cards Since each trial must end in success or failure, number of successes and number of failures adds up to total number of trials Probability is the number of times success occurred compared to the total number of trials Odds are the number of times success occurred compared to the number of times failure occurred
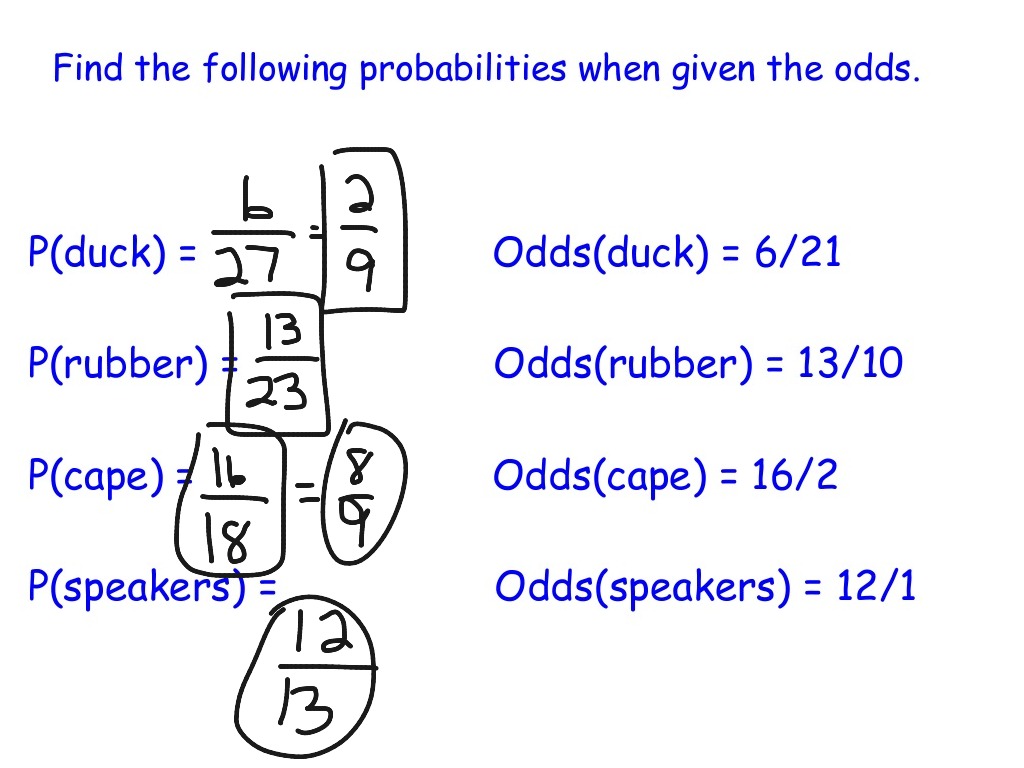



Probability Probability Vs Odds Lesson Math Statistics Showme




Odds Probability And The Lottery Lotterycodex
Odds vs Probability Odds and probability are both terms used to describe the likeliness for something to happen Many of us mix them up, but in fact, they are quite different, which is why we have added this article to our online guide section Without any numbers, the words can mean the same Probability is 1/4 while odds in favor are 1/3 You can see how mistakenly interchanging the terms could give the wrong information The 'odds in favor' of RED would be mathematically calculated by $latex Odds\_Favor (RED) = \frac {3 \ RED \ marbles} {9 \ NOT \ RED \ marbles} = 13&s=2$Odds vs Dealer Up Card The first odds chart shows what kind of advantage the player has vs the dealer based on what his up card is showing The first column in the chart is what card the dealer has showing after the cards have been dealt The second column of the table shows the dealer's probability of going bust based on each card
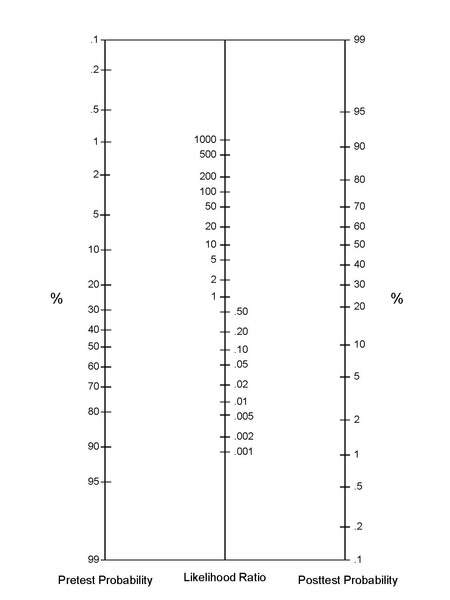



File Probability Nomogram Useful For Combining Probability And New Information That Changes Odds As Used In Evidence Based Medicine And Evidence Based Assessment 01 Pdf Wikimedia Commons



Faq How Do I Interpret Odds Ratios In Logistic Regression
Probability = 1/5 = 02; $\begingroup$ An odds ratio is the ratio of two odds Each individual odds value in the ratio can be converted to a probability as you propose, but I don't think that the same transformation applied to an odds ratio results in a probability value that has any easy interpretation $\endgroup$ – EdM Jan 29 ' at 1734Money Line Implied Probability The following chart shows how likely a team is to win based off the odds This is helpful in handicapping because you can see just what percentage of your wagers you need to win at each given money line in order to profit The left chart is to be used for favorites, the right for underdogs




Finding Probability Odds Changing Between Worksheets Handout Tpt




Lesson 0 11 Simple Probability And Odds The Probability Of An Event Is The Ratio Of The Number Of Favorable Outcomes For The Event To The Total Number
Probability % By convention only a set of fractions are used in fractional odds betting markets The set does not include exact mathematical equivalents to all possible decimal and American odds We use the closet fraction that is used in betting marketsFinding Value In A Moneyline Bet Using an implied probability calculator, you can convert the moneyline odds into an implied chance of winning for each Odds Odds seems less intuitive It is the ratio of the probability a thing will happen over the probability it won't In the spades example, the probability of drawing a spade is 025 The probability of not drawing a spade is 1 025 So the odds is 025/075 or 13 (or 033 or 1/3 pronounced 1 to 3 odds) Moving back and forth




11 6 Probability Involving Or And Not




Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1
Log_odds = seq(from =5,to =5,by =025) odds = exp(log_odds) # use 'plogis' function to calculate exp(x)/(1 exp(x)) p = plogis(log_odds) # use odds/(1odds) to calculate p a different way p2 =odds/(1odds) # store probability of failure (1p) q =1p # store log_odds and y in data frame for use with ggplot 1 The mathematical concept of odds is related to, yet distinct from the concept of probability In simplest terms, odds are a way of expressing the relationship between the number of favorable outcomes in a given situation versus the number of unfavorable outcomes Usually, this is expressed as a ratio (like 1 3 or 1/3) Know that odds tell you the likelihood of an outcome Odds represent which team, horse, or athlete has the highest probability of winning While there are different ways to write odds, they all indicate how likely one outcome is in comparison to another Ex When I flip a coin, it is just as likely that I flip heads as tails




11 6 Probability Involving Or And Not




Comparing Probability Odds For And Odds Against Youtube
To convert odds to probability, take the player's chance of winning, use it as the numerator and divide by the total number of chances, both winning and losing For example, if the odds are 4 to 1, the probability equals 1 / (1 4) = 1/5 or % Odds of 1 to 1 (50%) are called "evens," and a payout of 1 to 1 is called "even money"The probability of having the winning plate is 1 out of 25 Odds of winning = number of chances to win number of chances to draw other numbers Odds of winning = 124 (Read as "1 to 24") Odds of not winning = number of chances to draw other numbers number of chances to win Odds of not winning = 241 (Read as "24 to 1") As you can see, the idea of probability is relatively simple But the idea of odds, on the other hand, is a bit more complicatedmostly because there's more than one way to write them The most common way is what's called "bookmakers odds"



Ctspedia Ctspedia Oddsterm
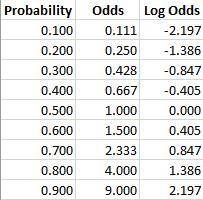



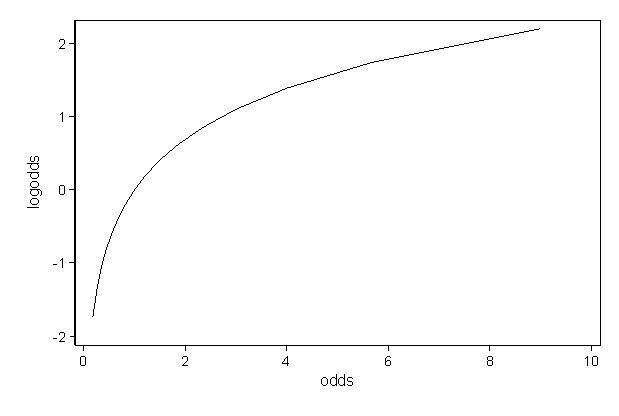
Log Odds Definition And Worked Statistics Problems
Posttest probability = Posttest odds / (Posttest odds 1) Fagan nomogram 3 The relation can also be estimated by a socalled Fagan nomogram (shown at right) by making a straight line from the point of the given pretest probability to the given likelihood ratio in their scales, which, in turn, estimates the posttest probability at the point A probability of 0 is the same as odds of 0 Probabilities between 0 and 05 equal odds less than 10 A probability of 05 is the same as odds of 10 Think of it this way The probability of flipping a coin to heads is 50%




Probability And Odds Worksheets Teaching Resources Tpt




11 6 Probability Involving Or And Not




Odds Vs Probabilities Odds Ratio In Spss Exp B Is An Odds Rather Than A Probability Odds Success Failure Probability Likelihood Of Success For Ppt Download




Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science




Poker Probability Wikipedia




Learn Odds In Favour And Odds Against In 3 Minutes




Calculating Probability And Odds How To Find The Odds Of Casino Games




Converting Probability To Odds Example Youtube




5 6 Probability And Odds Lesson




The Difference Between Relative Risk And Odds Ratios The Analysis Factor




How To Calculate Odds 11 Steps With Pictures Wikihow



Odds Likelihood Ratios Guide To Diagnostic Tests
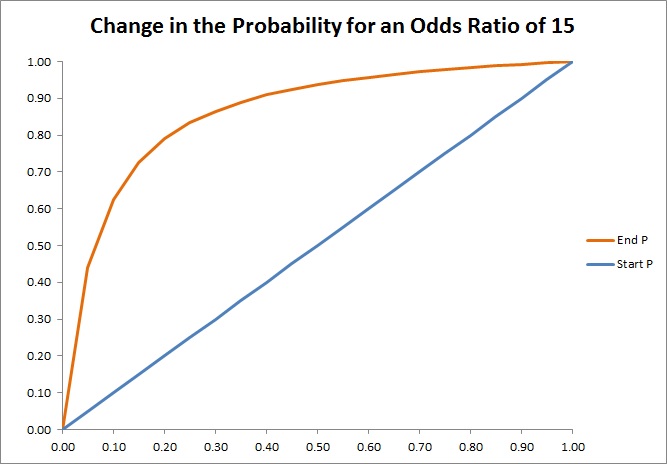



How To Convert Odds And Units To Probability Convert Odds To Percentage




Facing Page Probability Of Survival And Odds Ratios For Death Download Scientific Diagram




Logistic Regression 1 From Odds To Probability Dr Yury Zablotski
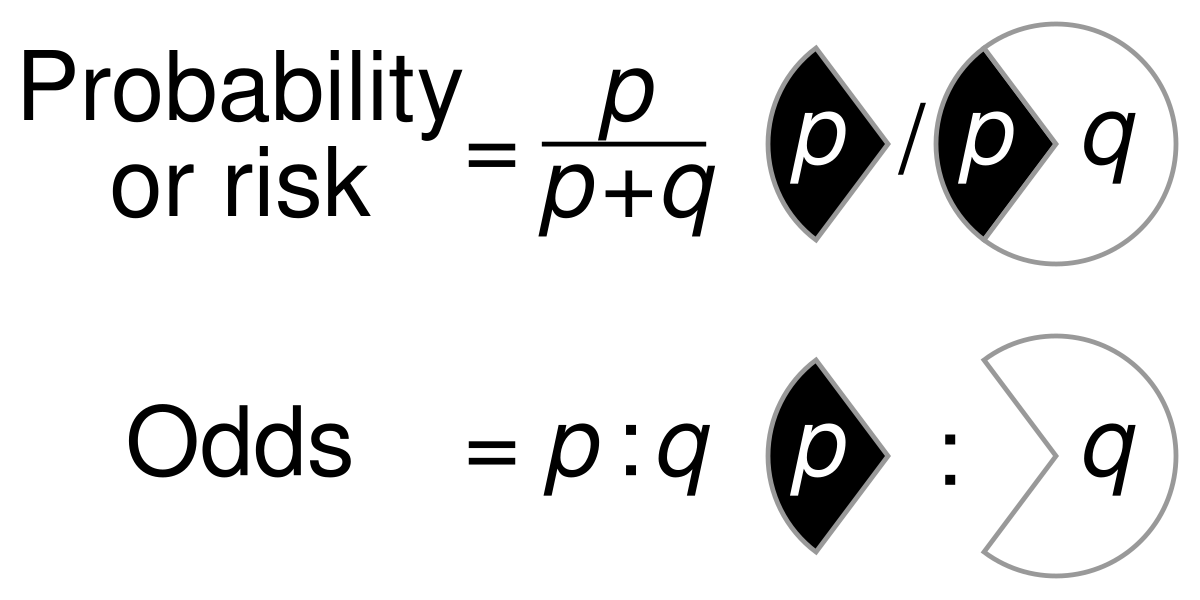



File Probability Vs Odds Svg Wikimedia Commons
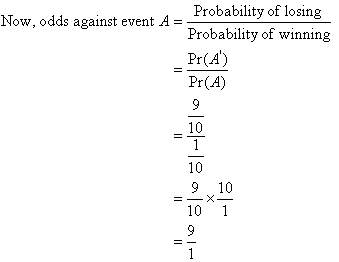



Odds



Odds Vs Risk Vantage Research




Pdf On Determining Probability Forecasts From Betting Odds Semantic Scholar




7 Facts About Probability And Odds That You Don T Know



2 Odds Ghci Grade 12 Mathematics Of Data Management
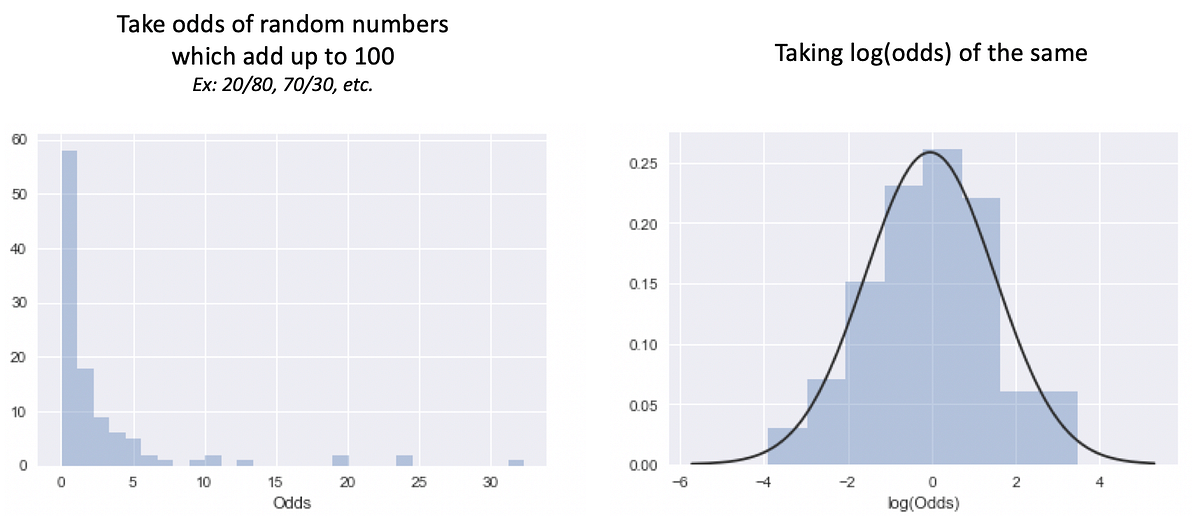



What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science
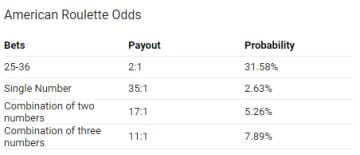



Odds Probability The Difference Explained With Examples



Odds Vs Probability Vs Chance Data Science Central



Probability Odds Lessons Blendspace




Relation Between Probability And Odds At Different Values Of Probability Download Scientific Diagram
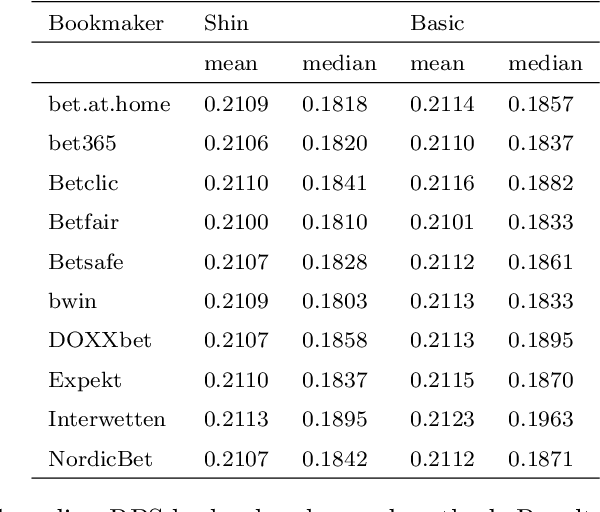



Pdf On Determining Probability Forecasts From Betting Odds Semantic Scholar




Odds Ratios Versus Relative Risk




Converting Between Probability And Odds Mathwoes Youtube




Estimated Z Score Odds Ratio And The Corresponding Probability For The Download Table




Odds Ratio The Odds Ratio Is Used To Find The By Analyttica Datalab Medium



The Difference Between Probability And Odds




Probability And Odds Quiz 13 Questions By Amy Harrison Tpt




What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science




Probability Vs Odds Youtube




Probability And Odds Youtube




Odds And Probability Definitions Key Difference Between Odds And Probability Comparison Chart Examples Ccss Math Answers
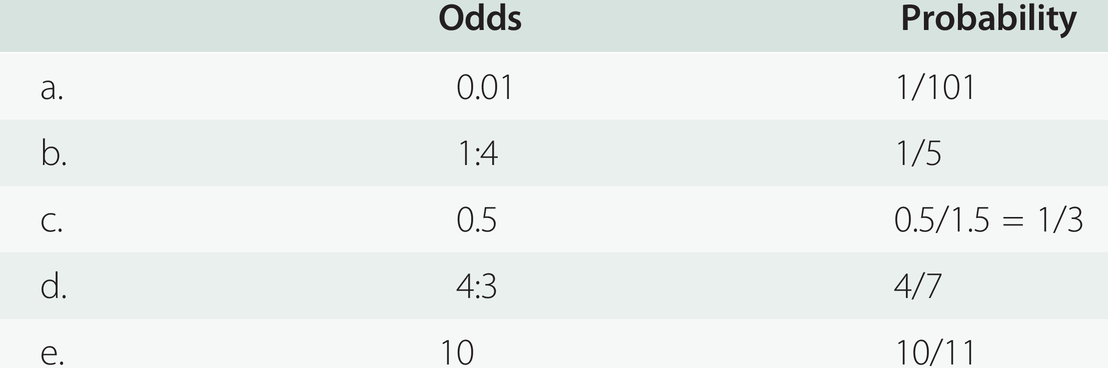



Answers To Odds Probability Conversions In Appendix 2 3 Evidence Based Diagnosis




Probability Vs Odds In Favour Or Against An Event Examples Youtube




Learn Odds In Favour And Odds Against In 3 Minutes




Mog Odds Probability Calculator Masters Of Gambling




What S The Difference Between Probability And Odds



Odds Vs Probability A Misunderstanding Elementsofai




Probability Vs Odds What S The Difference Learn It And By Z Ai Towards Data Science




Lecture 5 Basic Probability David R Merrell 90




Cureus What S The Risk Differentiating Risk Ratios Odds Ratios And Hazard Ratios




Difference Between Odds And Probability With Comparison Chart Key Differences




What Is An Odds Ratio And How Do I Interpret It Critical Appraisal




Section 11 6 Odds And Expectation Math In Our World Ppt Download
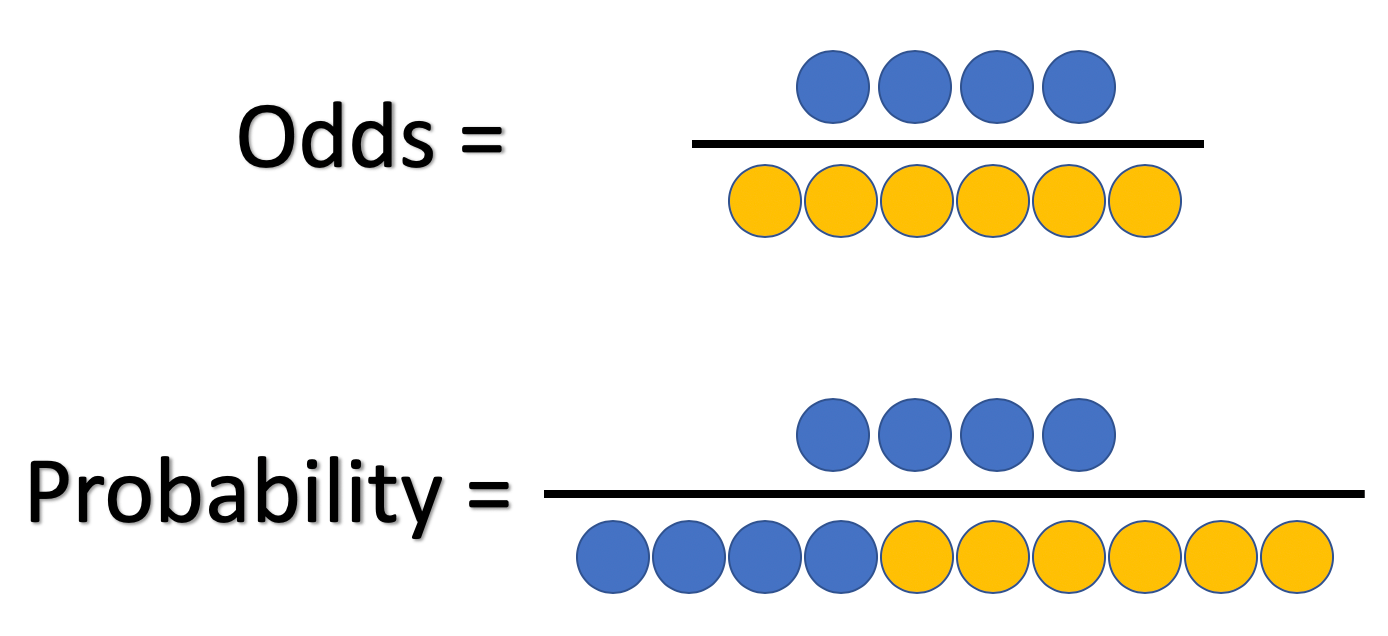



What And Why Of Log Odds What Are Log Odds And Why Are They By Piyush Agarwal Towards Data Science




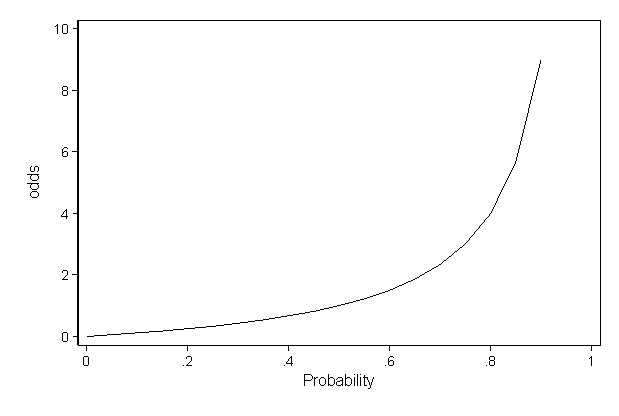
File Odds As Function Of Probability Svg Wikimedia Commons
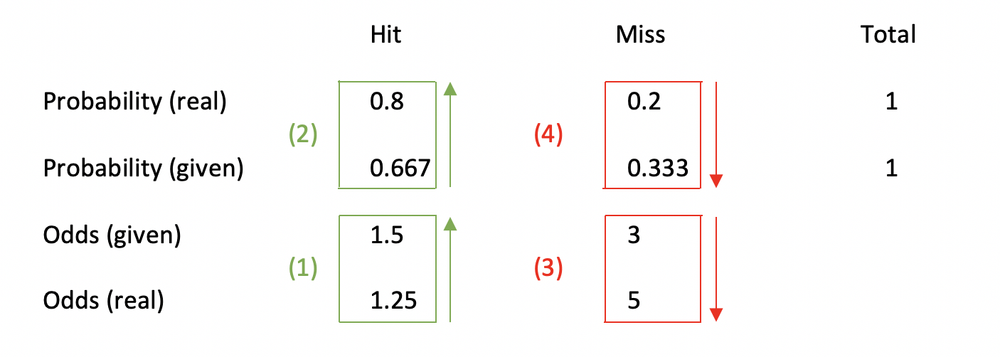



What Are Odds The Right Way To Look At Odds For Sports Betting



1




What Is A Probability And What Are Odds Core Im Podcast
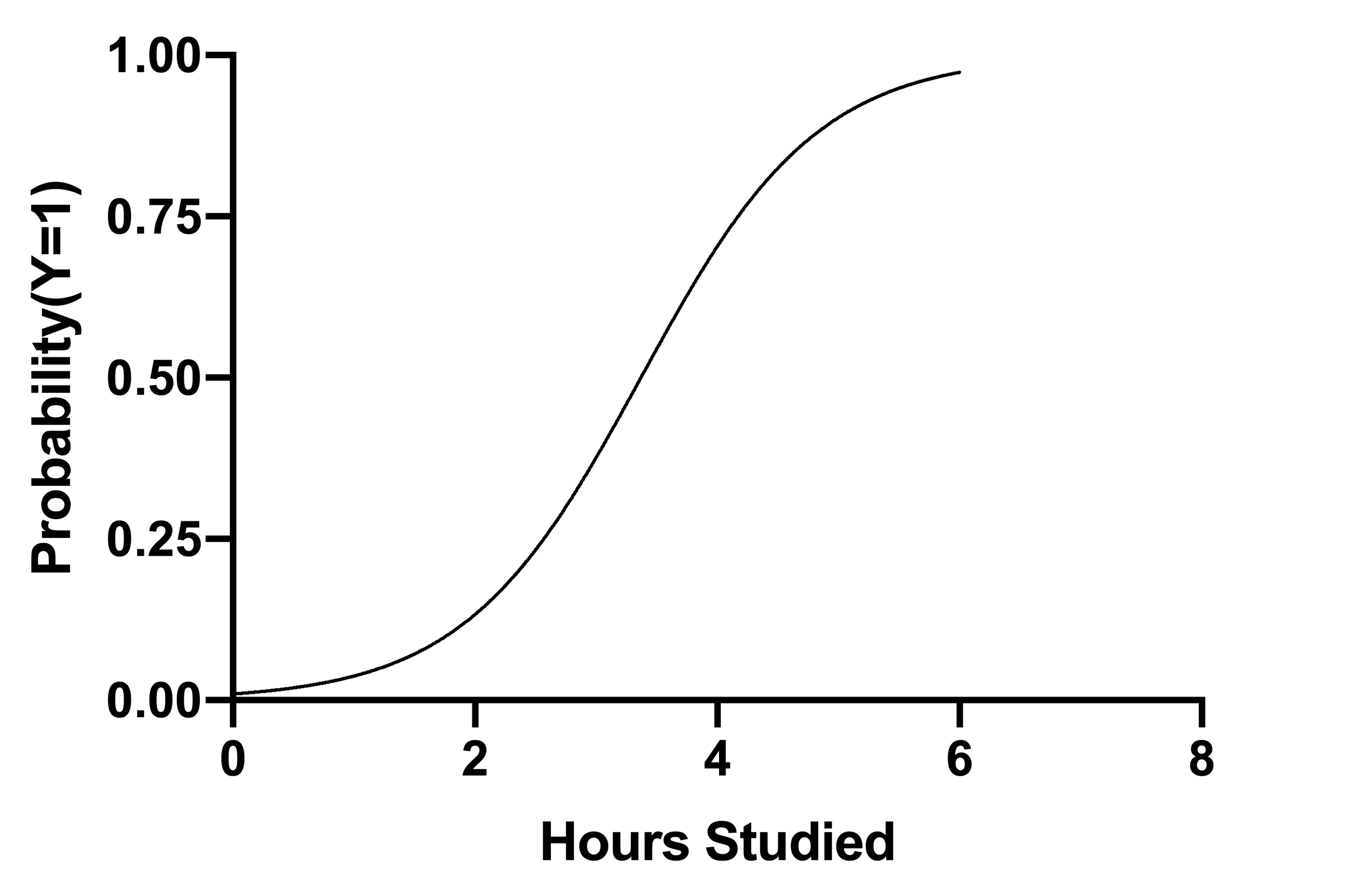



Graphpad Prism 9 Curve Fitting Guide Interpreting The Coefficient Estimates




Odds And Probability




Probability Theory How To Calculate The Odds Of Winning The Lottery You Should Read This Multilotto
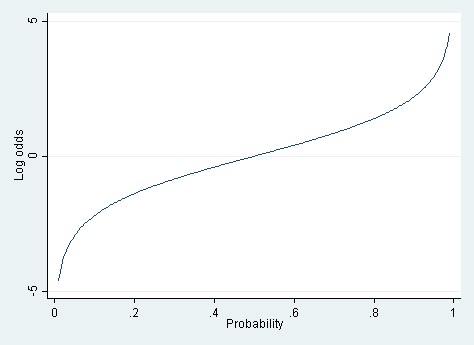



Linear Vs Logistic Probability Models Which Is Better And When Statistical Horizons




Into The Logistic Regression Towards Ai The Best Of Tech Science And Engineering




What Are The Odds That You Know About The Odds Analytics Vidhya
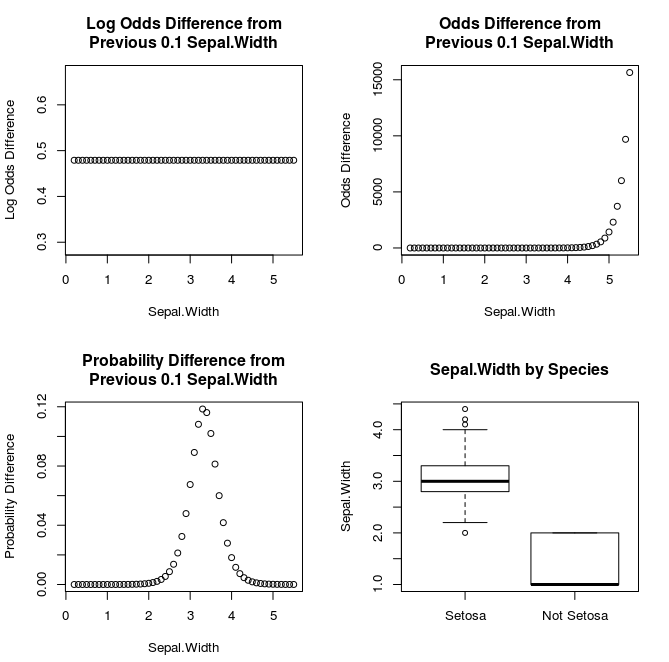



Why Saying A One Unit Increase Doesn T Work In Logistic Regression Learn By Marketing



Relative Risk Ratios And Odds Ratios




Assignment 4 1 Probability And Odds Continued 10 Chegg Com
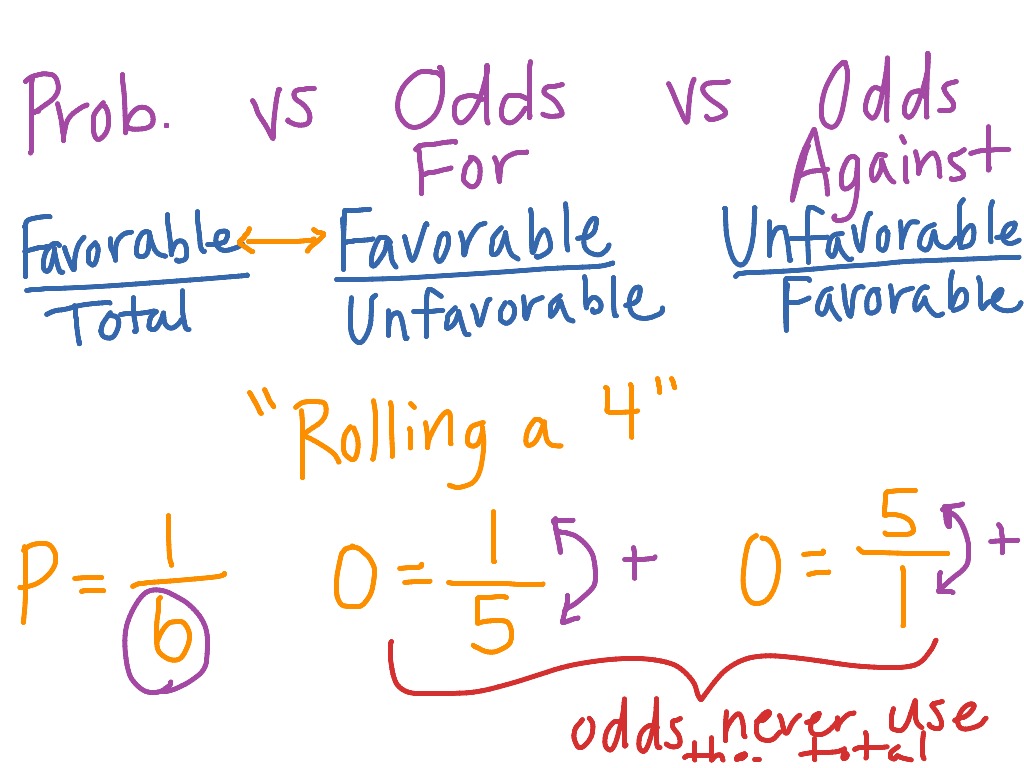



Odds Versus Probability Math Showme
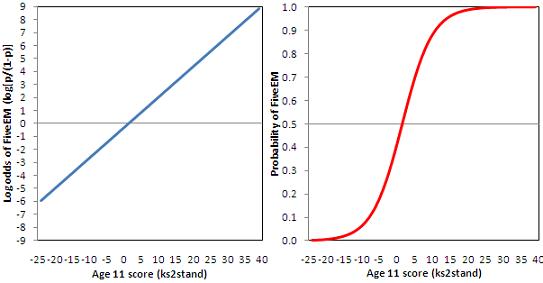



4 5 Interpreting Logistic Equations



Q Tbn And9gctxz8owky Sul84xtk4ggzacxwhkmhguhlxwyjj9avufagdrhwm Usqp Cau




Simple Probability Definition Probability The Chance Some Event




Counting And Probability Lesson 5 Probability And Odds



Faq How Do I Interpret Odds Ratios In Logistic Regression



1




Probability And Odds Math Odds Showme



Ctspedia Ctspedia Oddsterm




9 2 Binary Logistic Regression R For Health Data Science




Probability And Odds Pptx Powerpoint




Math 30 2 Probability Odds Acceptable Standards 50 79 The Student Can Express Odds For Or Odds Against As A Probability Determine The Probability Ppt Download




How To Calculate Odds Ratios And Probabilities In Case Control Studies Cross Validated



Definition And Calculation Of Odds Ratio Relative Risk Stomp On Step1



How To Remember The Differences Between Odds Ratio Hazard Ratio And Likelihood Ratio And In What Instances They Should Be Applied Quora



Odds Vs Probability Casino Spies




Webinar Recording Signup



1



Ppt Conditional Probability Powerpoint Presentation Free Download Id



0 件のコメント:
コメントを投稿